Skip to contents

Interaction and uncertainty

Kevin Cazelles

23-02-2024

analyse_uncertainty.Rmd

Study System

Here we consider one system that has 5 species and consists of two linear chains with one top predator linking the two.

## $A
##      [,1] [,2] [,3] [,4] [,5]
## [1,]   -1    0   -1    0    0
## [2,]    0   -1    0   -1    0
## [3,]    1    0    0    0   -1
## [4,]    0    1    0    0   -1
## [5,]    0    0    1    1    0
## 
## $B
## [1] 10000  1000   200   100    20
## 
## $R
## [1]   500   100  -500  -100 -1000
## 
## $U
##    row col unknown value  name
## 1    1   1    TRUE    -1 a_1_1
## 2    3   1    TRUE     1 a_3_1
## 3    2   2    TRUE    -1 a_2_2
## 4    4   2    TRUE     1 a_4_2
## 5    1   3    TRUE    -1 a_1_3
## 6    5   3    TRUE     1 a_5_3
## 7    2   4    TRUE    -1 a_2_4
## 8    5   4    TRUE     1 a_5_4
## 9    3   5    TRUE    -1 a_3_5
## 10   4   5    TRUE    -1 a_4_5
## 
## $sdB
## NULL
## 
## $model
## function (t, y, pars) 
## {
##     return(list((pars$A %*% y + pars$R) * y))
## }
## <bytecode: 0x561950b6ea48>
## <environment: namespace:fwebinfr>
## 
## attr(,"class")
## [1] "fw_problem"

Here is the dynamics of the system.

## Using "tree" as default layout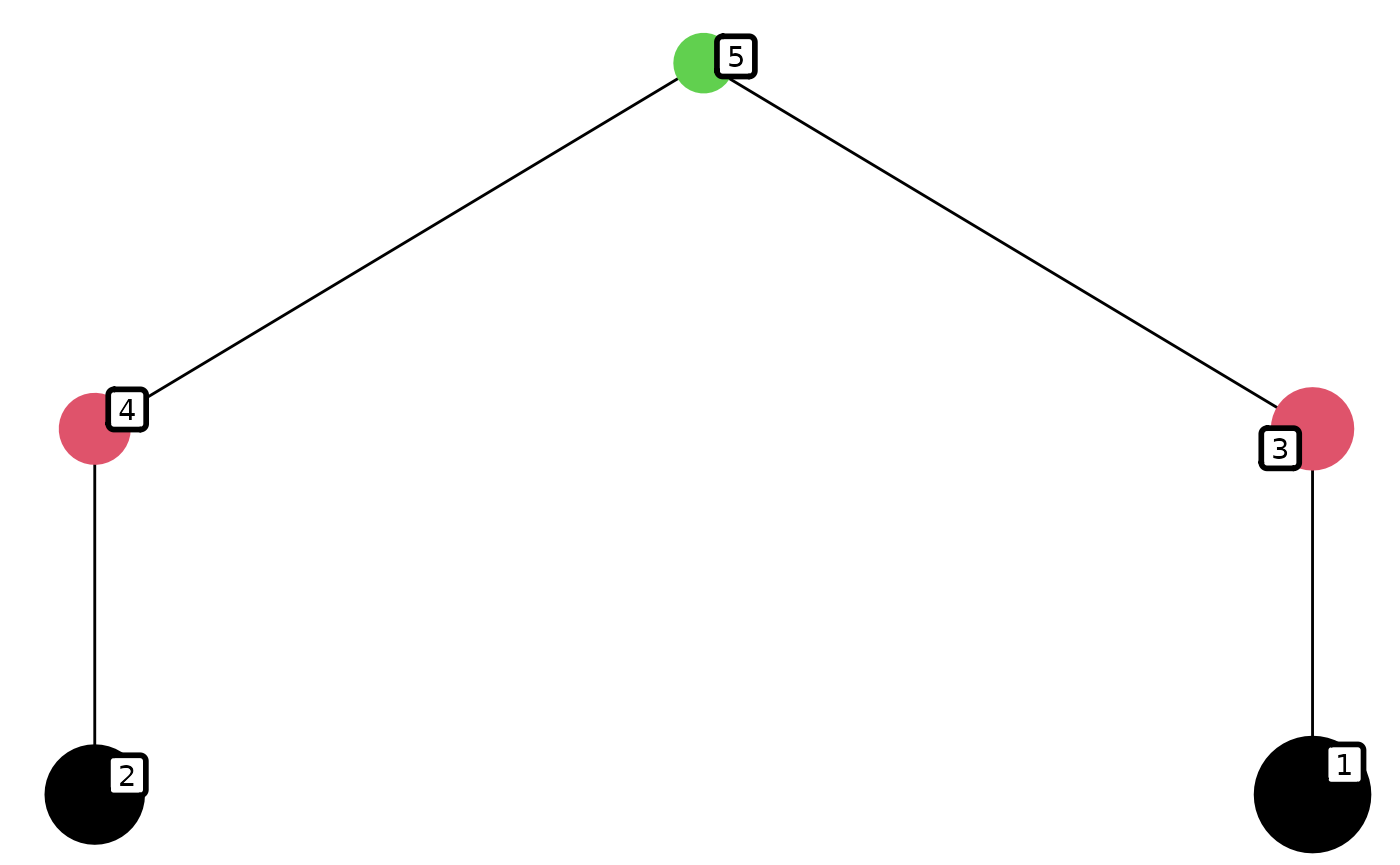

Basic inference

Now, we call fw_infer() to predict interaction strengths.

res <- net |> fw_infer()
## Warning in lsei(E = E, F = F, G = G, H = H): No equalities - setting type = 2
head(res$prediction)
##         a_1_1      a_3_1      a_2_2     a_4_2      a_1_3     a_5_3     a_2_4
## 1 0.048841634 0.05791831 0.08583662 0.1416338 0.05791831 3.9591553 0.1416338
## 2 0.001444207 0.62064003 0.06412953 0.3566577 2.42778966 1.3541516 0.3587047
## 3 0.010520594 0.34932731 0.03826696 0.4697553 1.97397028 1.5340412 0.6173304
## 4 0.007669695 0.46459334 0.05780077 0.3757557 2.11651526 1.1434280 0.4219923
## 5 0.011821589 0.69398904 0.04785023 0.4410869 1.90892053 1.9397128 0.5214977
## 6 0.015781313 0.64624097 0.03254650 0.3079886 1.71093434 0.5958955 0.6745350
##      a_5_4      a_3_5     a_4_5 leading_ev
## 1 2.081689   3.959155  2.081689  -4.819539
## 2 7.291697 285.320017 12.832883  -4.638453
## 3 6.931918 149.663654 18.487765 -23.688365
## 4 7.713144 207.296670 13.787785 -15.378358
## 5 6.120574 321.994521 17.054347 -29.064702
## 6 8.808209 298.120484 10.399432 -20.767728

Let’s visualize the range of interaction strength and stability.

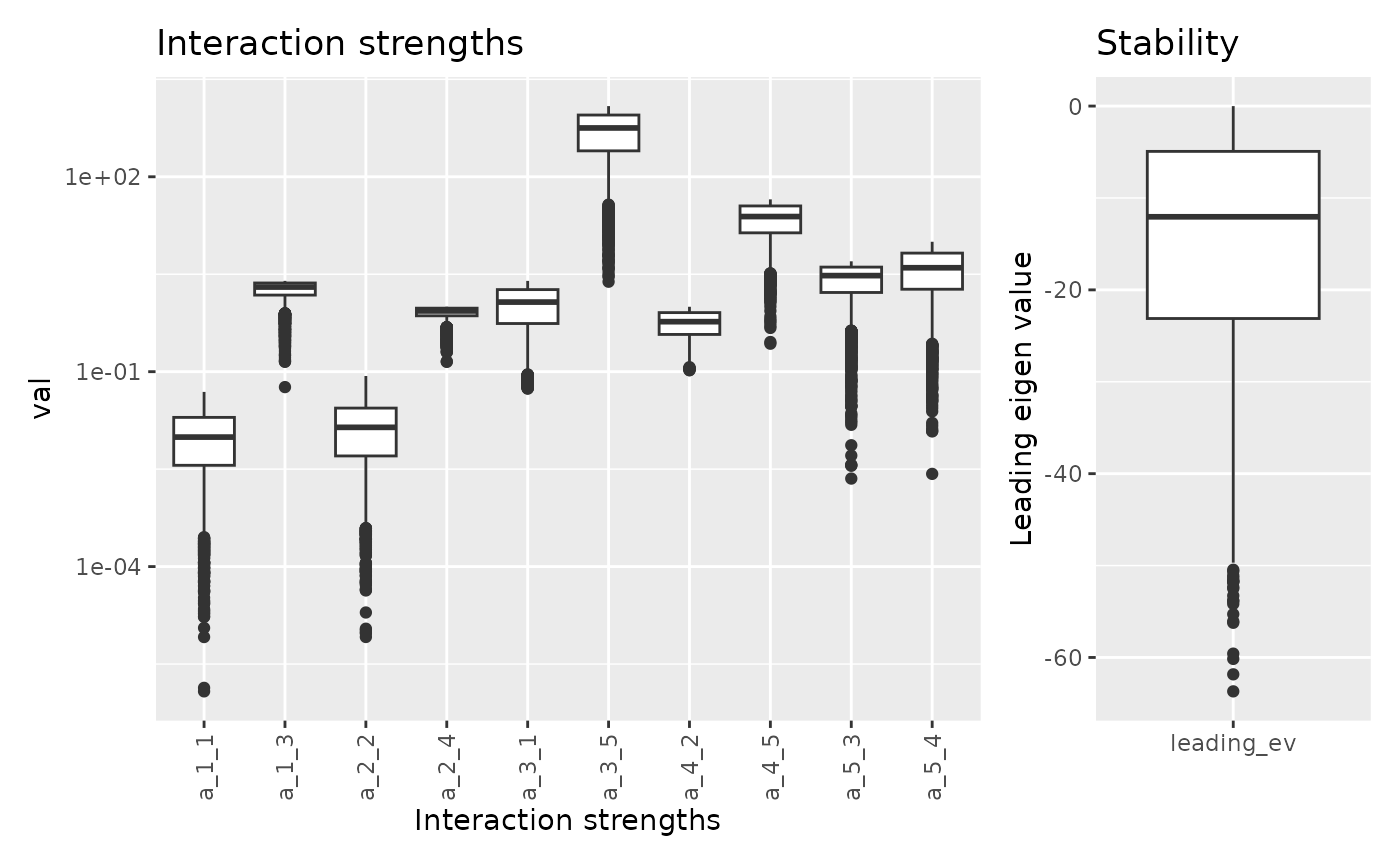
fw_range_compare_plot(res, show_lev = FALSE)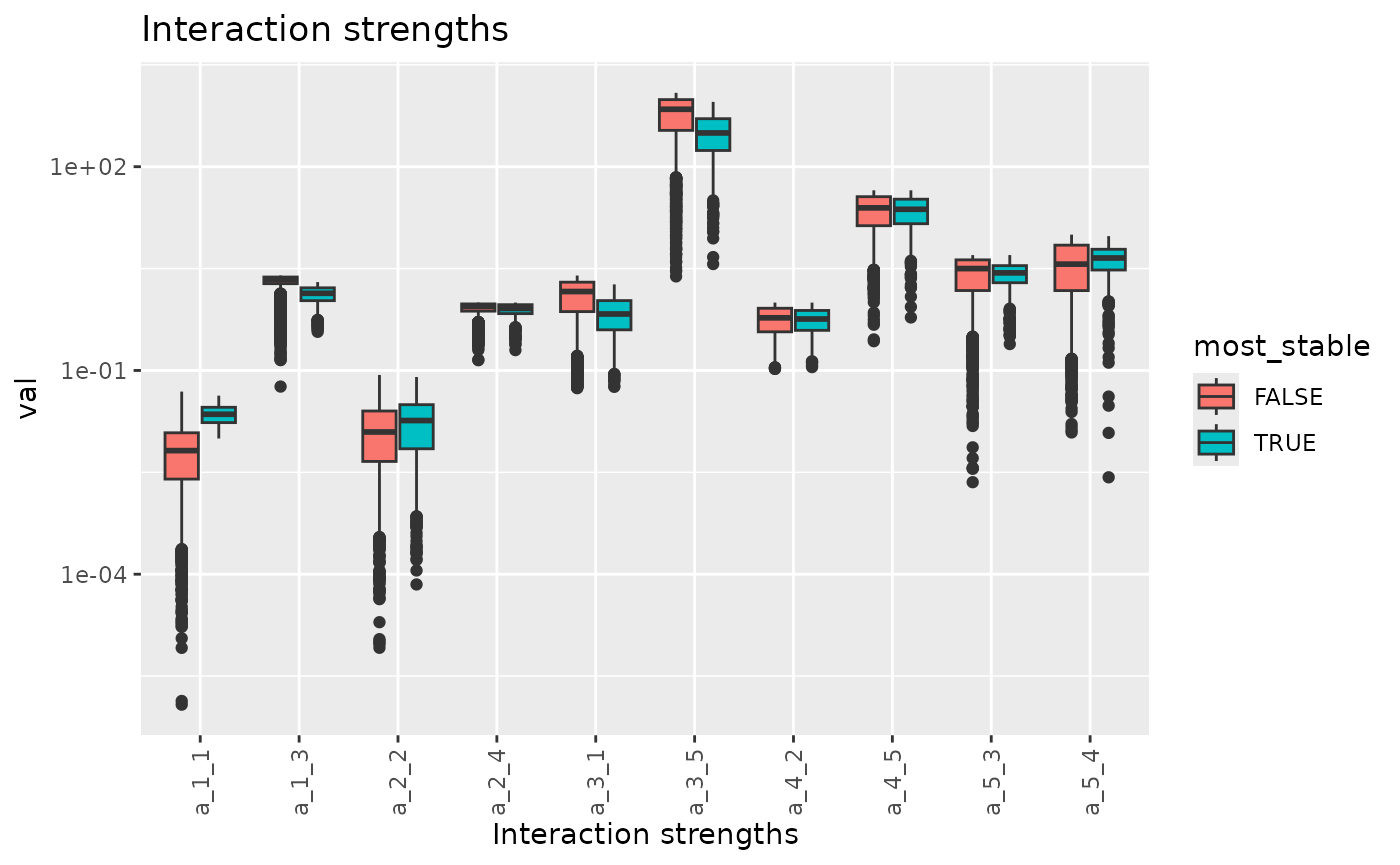

We can plot the dynamics for the most and the least stable systems.

net_most_stable <- fw_model(
  A = fw_predict_A(res, which.min(res$prediction$leading_ev)),
  B = fw_predict_B(res, which.min(res$prediction$leading_ev)),
  R = net$R
)
net_least_stable <- fw_model(
  A = fw_predict_A(res, which.max(res$prediction$leading_ev)),
  B = fw_predict_B(res, which.max(res$prediction$leading_ev)),
  R = net$R
)

p1 <- fw_ode_plot(net_most_stable, net$B/1.5, seq(0, 2, 0.0001)) +
  ggtitle("Minimum leading eigen value (most stable)") 
p2 <- fw_ode_plot(net_least_stable, net$B/1.5, seq(0, 2, 0.0001)) +
  ggtitle("Maximum leading eigen value (least stable)")
p1 / p2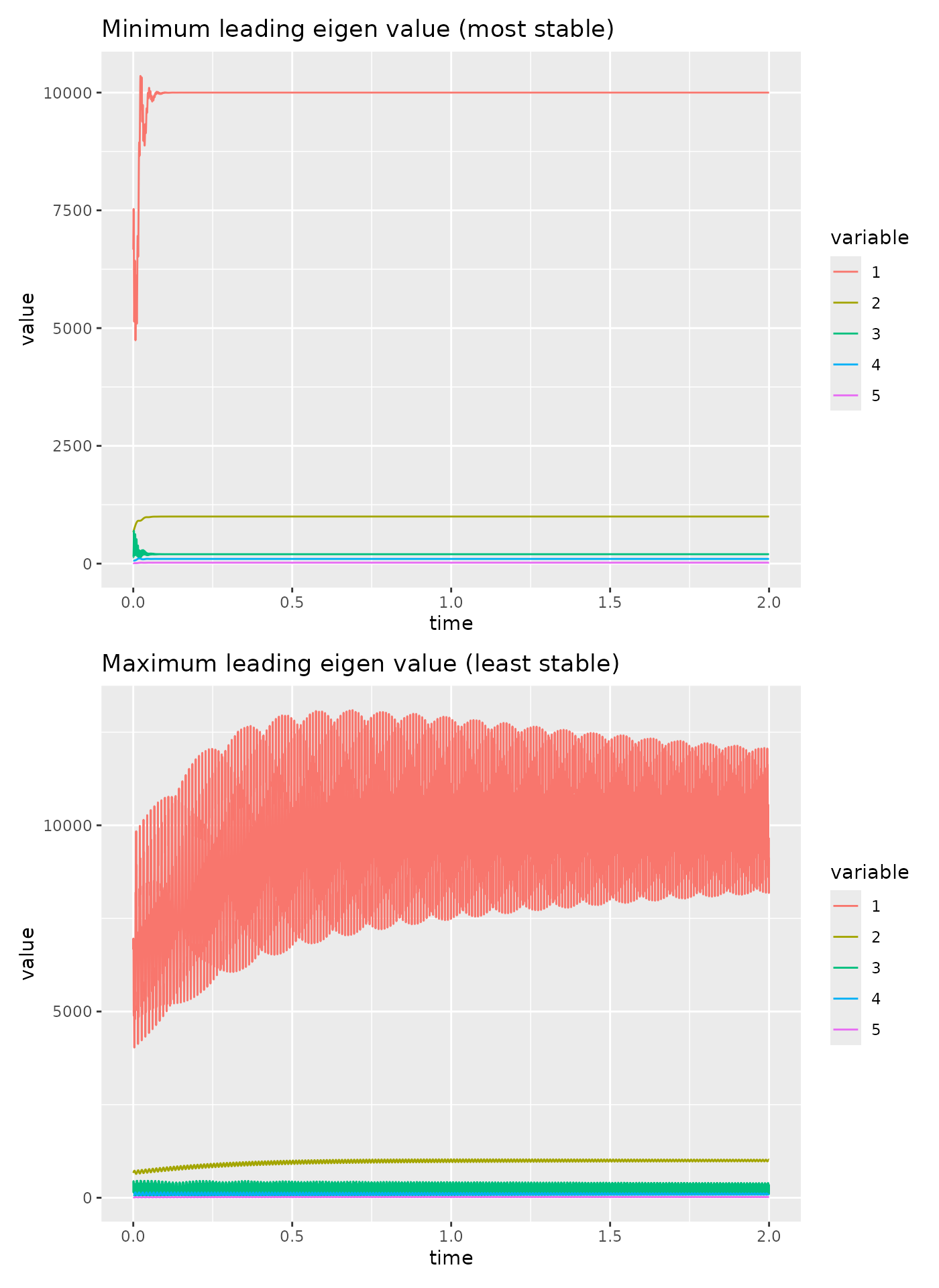

Narrowing down uncertainty

Let’s fix A[5, 3] to the mean of sampled values and observed the new range of parameters values.

## Warning in lsei(E = E, F = F, G = G, H = H): No equalities - setting type = 2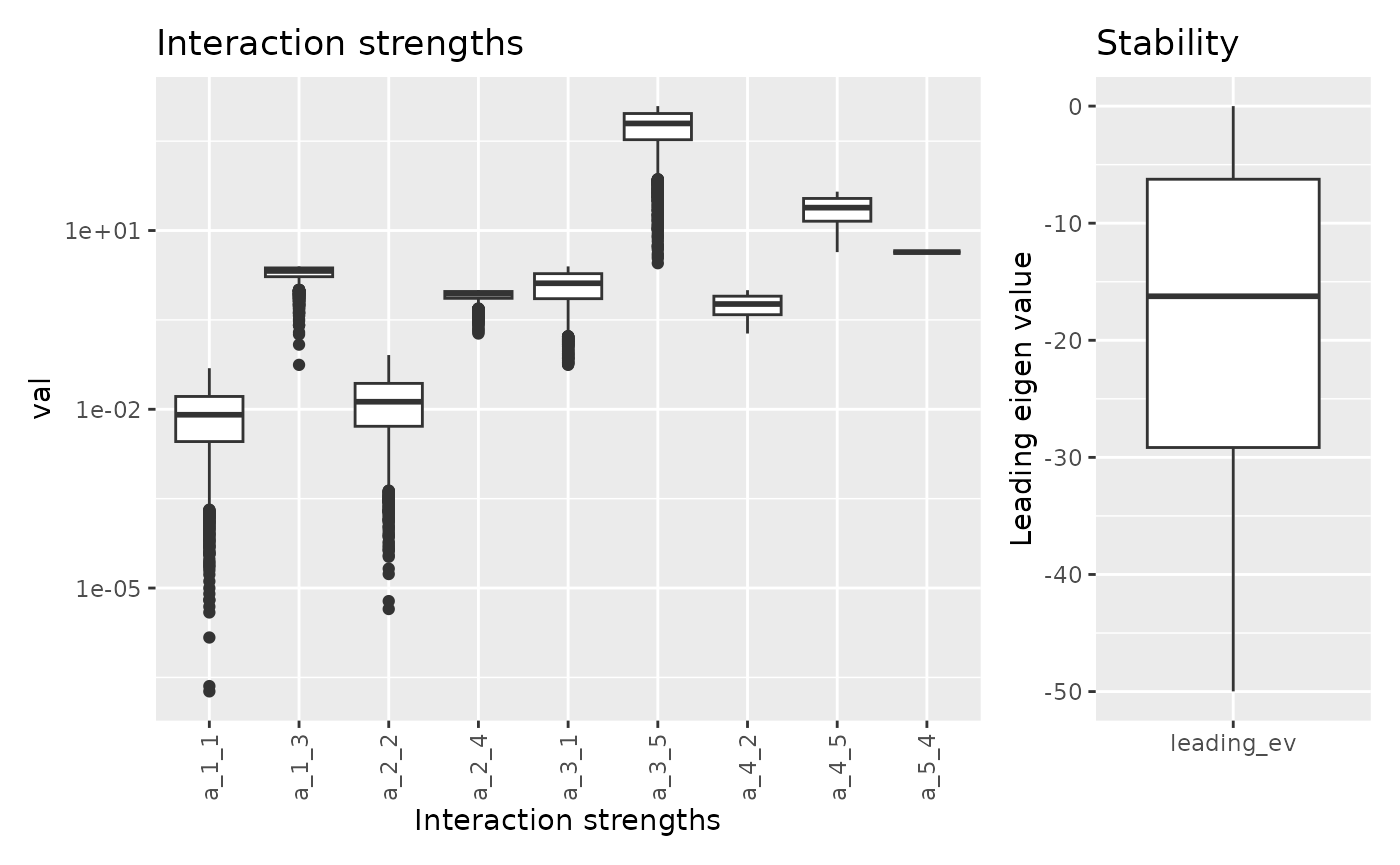

Let’s do the same changes but this time for A[3, 1]

## Warning in lsei(E = E, F = F, G = G, H = H): No equalities - setting type = 2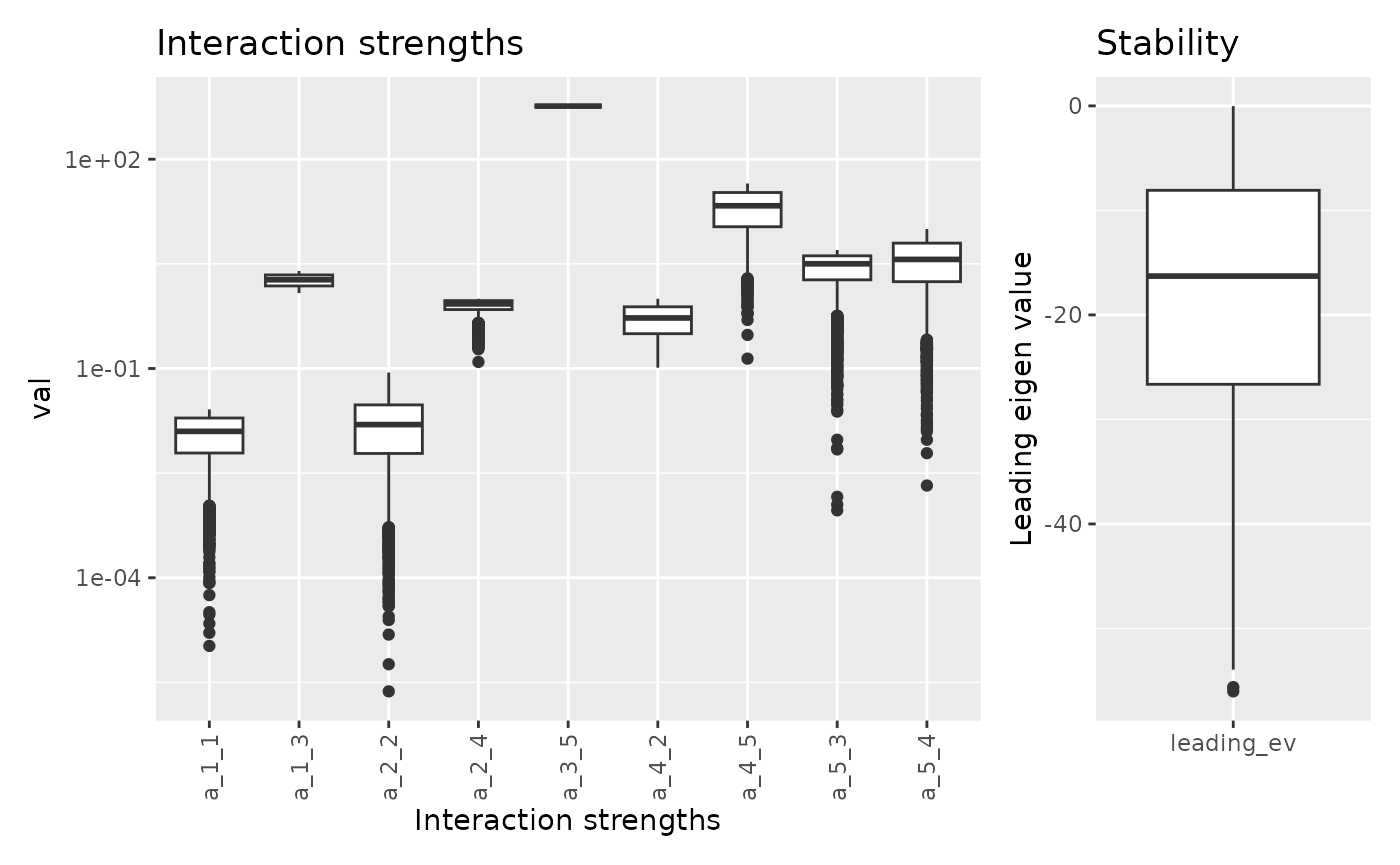

Combining the two:

## Warning in lsei(E = E, F = F, G = G, H = H): No equalities - setting type = 2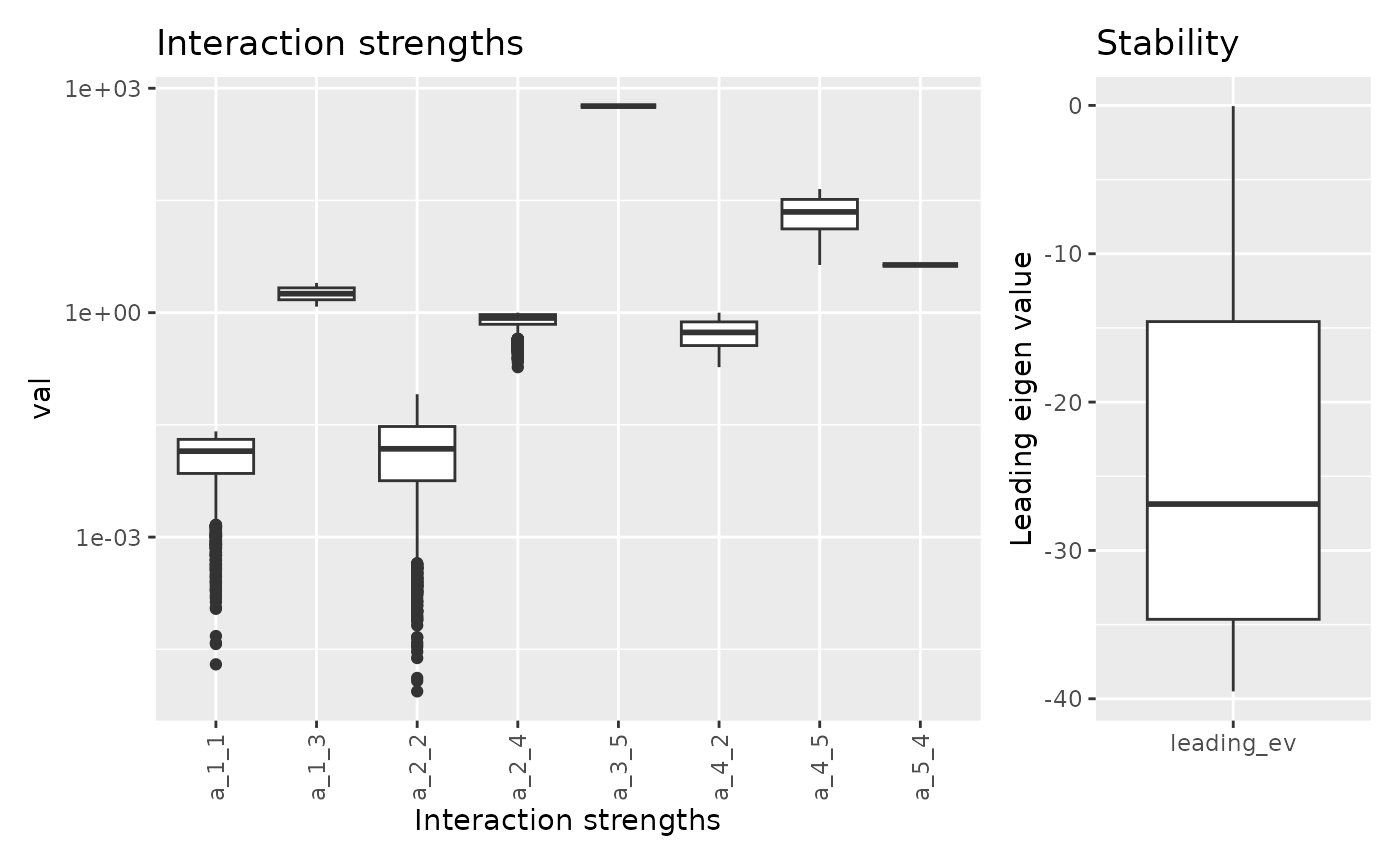

Imcreasing one interaction strenght

Here we increase A[3, 1] from 0.1 to 2.5.

## Warning in scale_y_continuous(trans = "log10"): log-10
## transformation introduced infinite values.
## Warning: Removed 3000 rows containing non-finite outside the scale range
## (`stat_boxplot()`).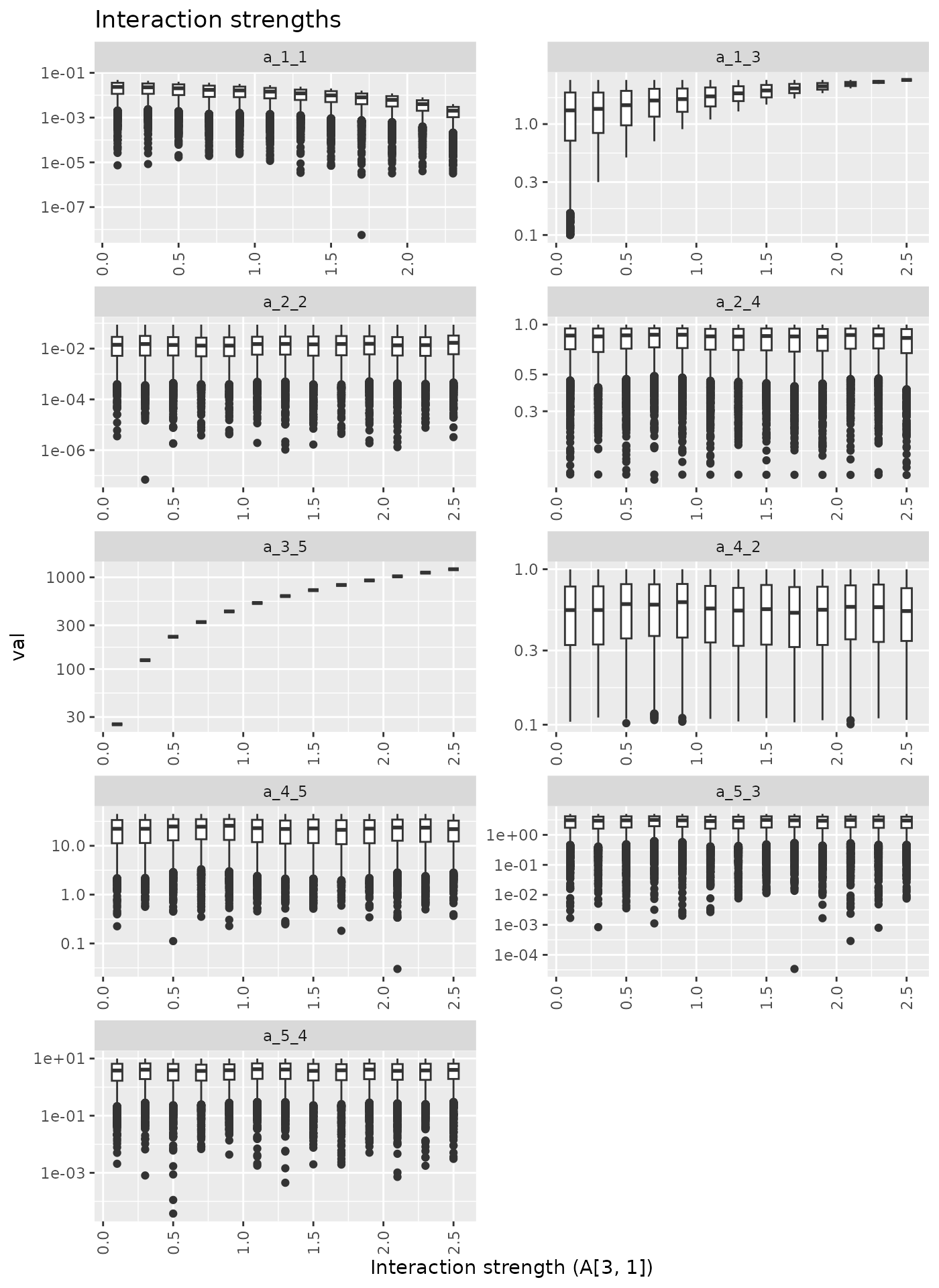

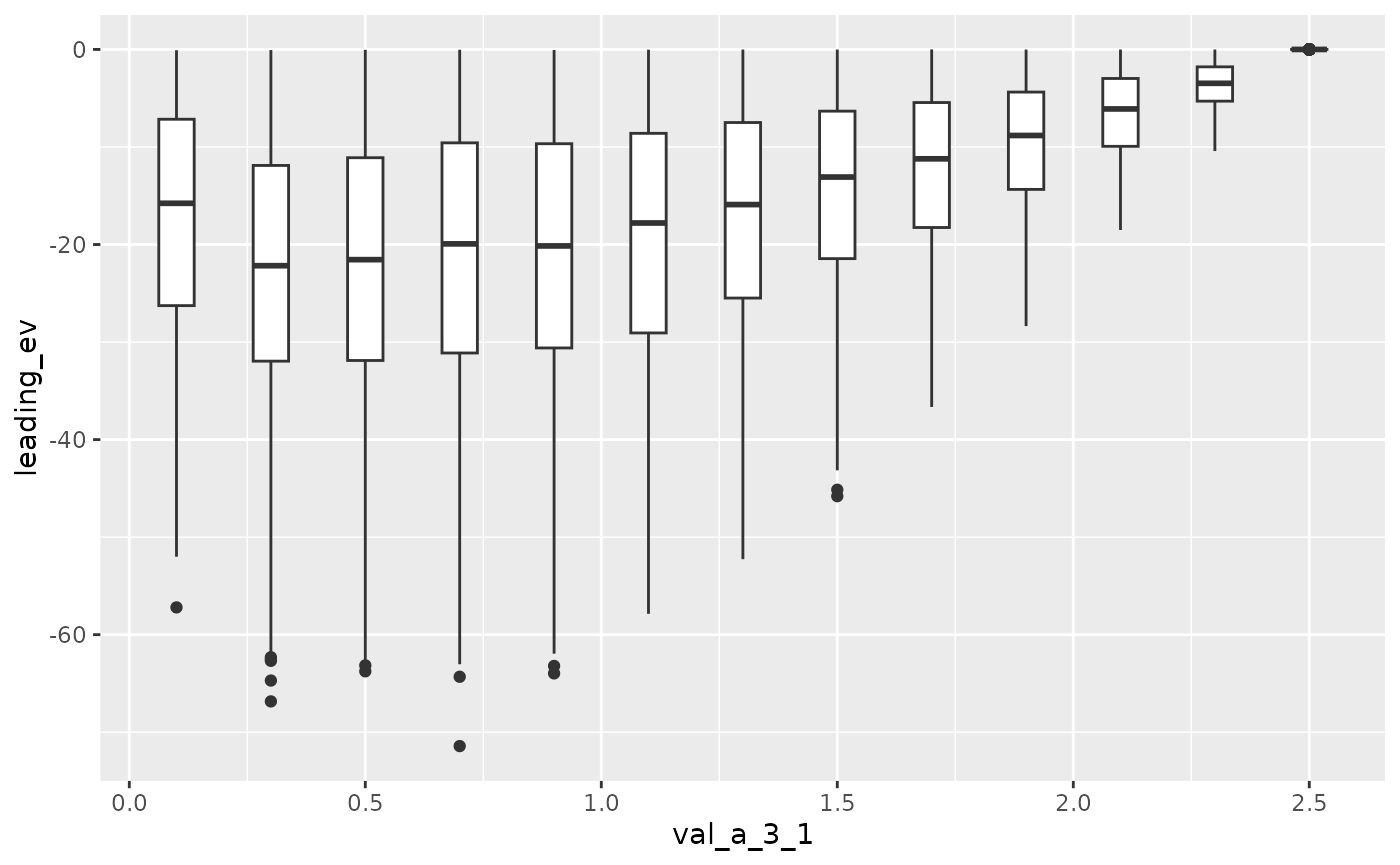
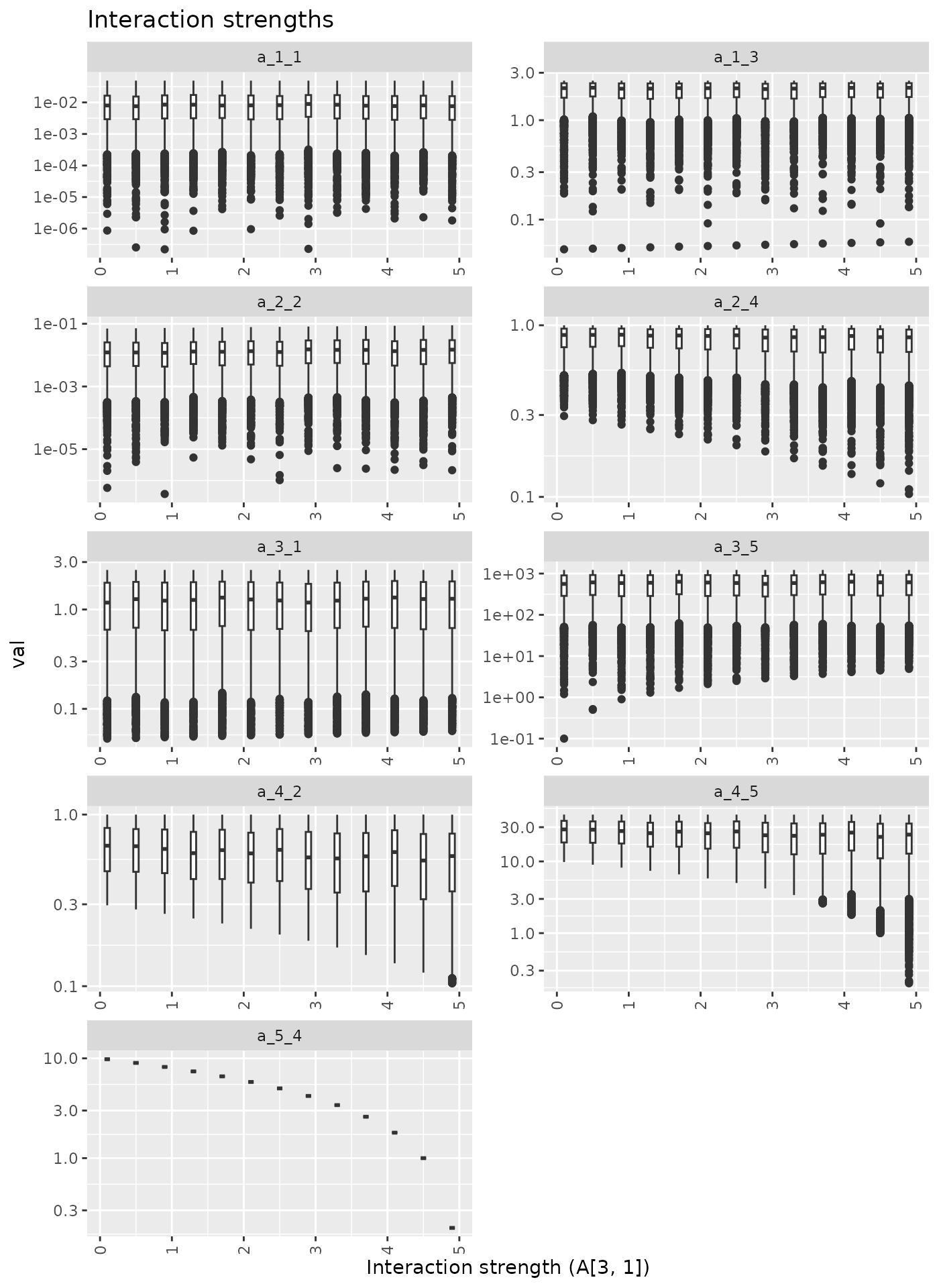
Now we increase A[5, 3] from 0.1 to 4.9.

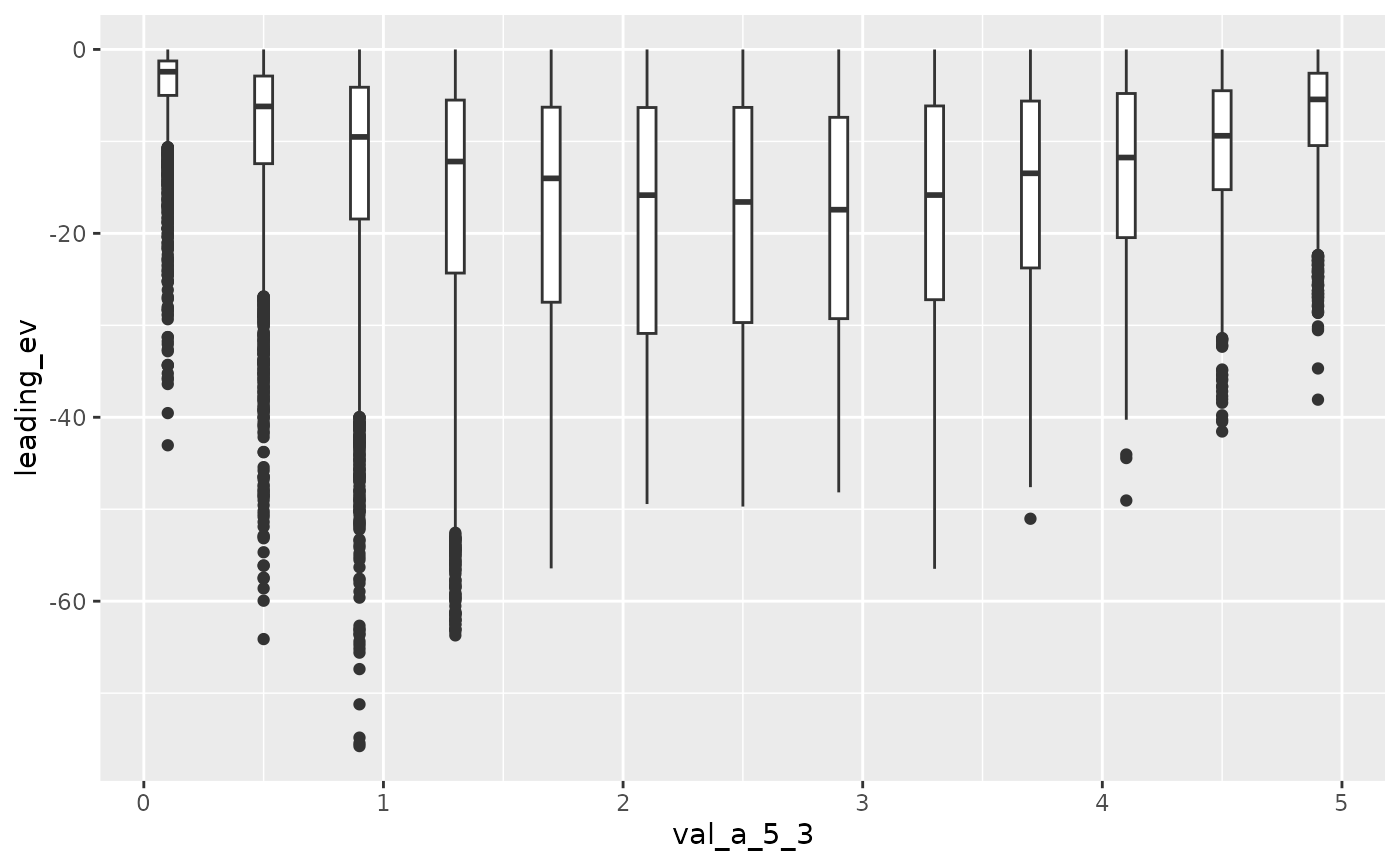
Now Here we increase A[3, 1] the from 0.1 to 2.5.